Deshbandhucollege Ac In
Answer (1 of 3) (2x y) dx (4x y 6) dy = 0 Find substitutions u, t to remove the (6) y = u a, x = t b \frac{du}{dt} = \frac{d(u a)}{d(t b)} = \frac{dy}{dx} Match the constants a, b by making a system of linear equations Each equation is an expression in parentheses set equa2x 2y dy dx = 0 Collect all the dy dx on one side y dy dx = −x Solve for dy dx dy dx = −x y The Chain Rule Using dy dx Let's look more closely at how d dx (y 2) becomes 2y dy dx The Chain Rule says du dx = du dy dy dx Substitute in u = y 2 d dx (y 2) = d dy (y 2) dy dx And then d dx (y 2) = 2y dy dx Basically, all we did was differentiate with respect to y and multiply by dy
Y 4x y dx-2 x 2-y dy 0
Y 4x y dx-2 x 2-y dy 0-Question find the relation between x and yB √(x2 y2 y) = C;
Utdallas Edu
Answer The equation is M(x,y)dx N(x,y)dy =0 with M = 4xy y^2 , M_y = 4x 2y N = 2y 2x^2 , N_x = 4x # M_y The equation is not exact , but (N_x M_y)/M = 2/y , depends only on y The integrating factor is 1/y^2 and leads to the equation P(x,y)dx Q(x,y)dy =0 , with P = 4x/y 1Y = 4x/(x^25) a) Find dy/dx, writing your answer as a single fraction in its simplest form b) Hence find the set of values of x for which dy/dx < 0 a) We need to differentiate this equation using the quotient rule (Given that it is a fraction with an x term on both the top and bottom of the fraction) We assign the numerator and denominator as follows u = 4x, v = x^25, and so using theProblem Answer The solution is √(x2 y2 ) y = C View Solution Latest Problem Solving in Differential Equations More Questions in Differential Equations Online Questions and Answers in Differential Equations MCQ in Differential Equations
4x 2 y 3 4xy 2 y = 0To find dy/dx we need to differentiate all the terms in the equation As you may notice the x's and y's are mixed together so we will have to use implicit differentiation Since we are differentiating in terms of x, all of the x terms can be differentiated as usual, whilst the y terms will be followed by a dy/dx The first two terms are more straight forward to dealTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `x(1y^2)dxy(1x^2) dy=0` x 2 4x 4 y(x 2)dy/dx y 2 = 0 (x > 0) which is further simplified as follows (x 2) 2 y(x 2)dy/dx y 2 = 0 Substituting x 2 = t, we get dx/dy = dt/dy which passes through the point (1, 3) Therefore, from Eq (1), we get That is, the solution curve intersects y = (x 2) exactly at one point and not at two points Therefore, option (A) is correct and option (B) is
Y 4x y dx-2 x 2-y dy 0のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 | 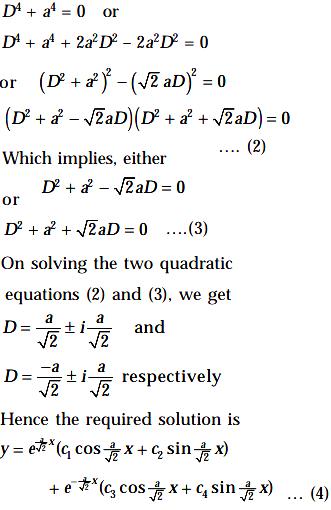 |  |
 |  |  |
「Y 4x y dx-2 x 2-y dy 0」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「Y 4x y dx-2 x 2-y dy 0」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
「Y 4x y dx-2 x 2-y dy 0」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 | ||
「Y 4x y dx-2 x 2-y dy 0」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
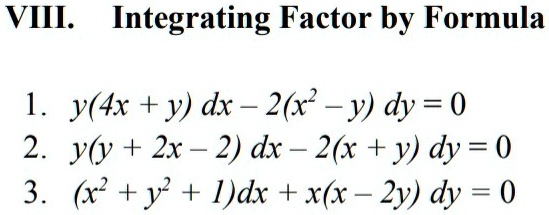 |  | |
「Y 4x y dx-2 x 2-y dy 0」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「Y 4x y dx-2 x 2-y dy 0」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
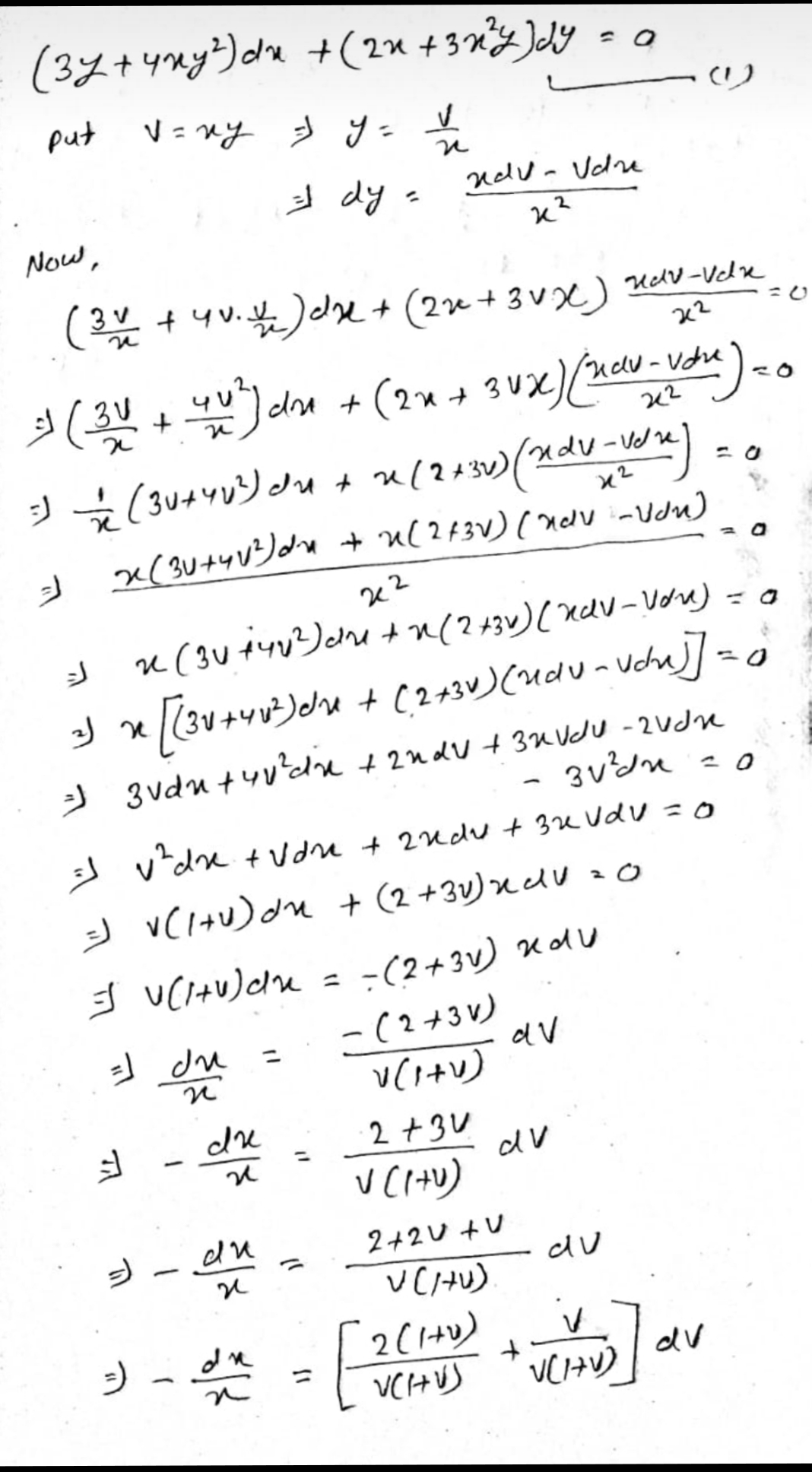 |  | |
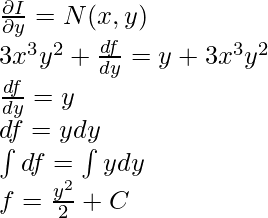 | ||
「Y 4x y dx-2 x 2-y dy 0」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 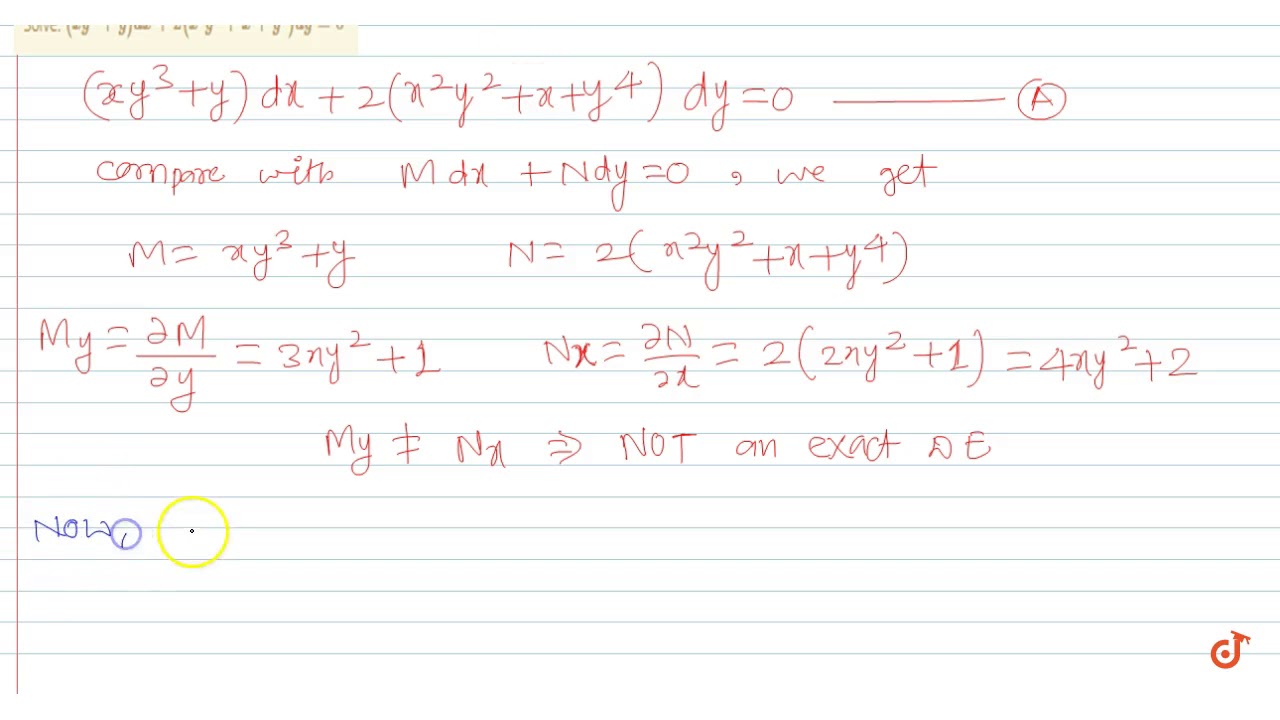 |  |
 | ||
 |  |  |
「Y 4x y dx-2 x 2-y dy 0」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  | |
「Y 4x y dx-2 x 2-y dy 0」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | 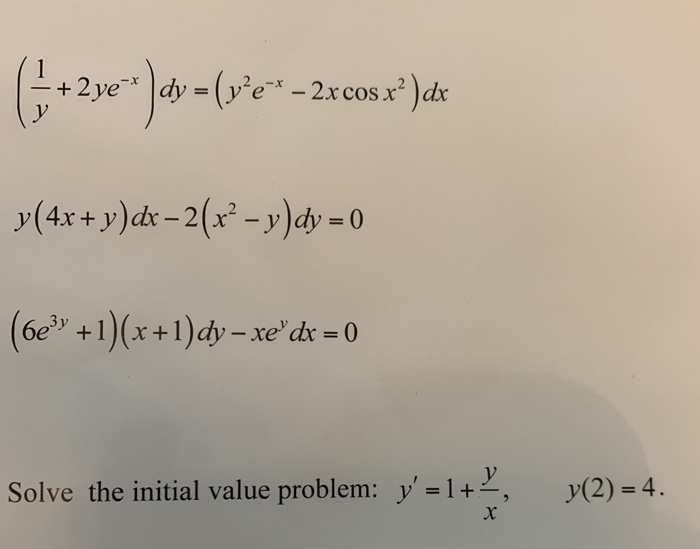 |
「Y 4x y dx-2 x 2-y dy 0」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | 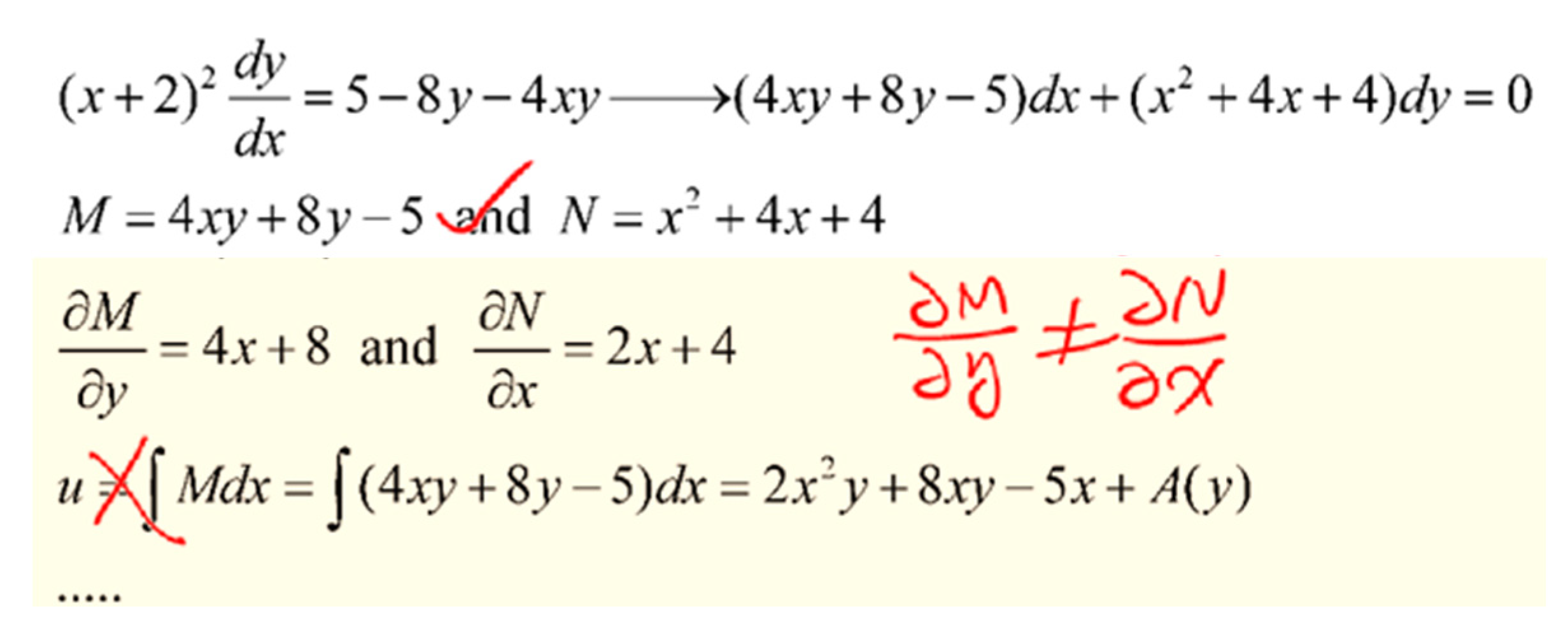 |
 |  |  |
「Y 4x y dx-2 x 2-y dy 0」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |
Differentiate using the Power Rule which states that d d x x n d d x x n is n x n − 1 n x n 1 where n = 2 n = 2 Multiply 2 2 by − 1 1 Reform the equation by setting the left side equal to the right side Reorder factors in −2e−x2 x 2 e x 2 x Replace y' y ′ with dy dx d y d xSimple and best practice solution for (2xy3x^2)dx(x^2y)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it
Incoming Term: y 4x y dx-2 x 2-y dy 0,




0 件のコメント:
コメントを投稿